한양대학교 알고리즘 동아리인 ALOHA에 들어가게 되었다. 고급반은 매주 셋 하나를 잡고 같이 도는 활동을 한다는 것 같다. 이번 셋은 gggkik의 셋인데, 특이사항으론 셋의 문제를 전부 본인이 출제한 문제로 냈다. -3문제를 가장 먼저 해결한 사람에겐 밥을 사준다는 상품이 걸려있었고, 참을 수 없었다.

(A번) DKSH 찾기 https://www.acmicpc.net/problem/29766
문자열의 길이도 작고, DKSH도 작기에 나이브한 문자열 비교 알고리즘을 짜면 된다.
(B번) 운동회 https://www.acmicpc.net/problem/25425
지문이 해석이 어려울 수 있는데, " 준혁이의 지금 가질 수 있는 등수는 (준혁의 팀을 제외한 남아있는 팀의 수 + 1)과 같다." 가 핵심이다. 팀을 최대한 죽이려면 한 팀씩 다 죽이면 되고, 살리려면 한 팀당 한명씩 제거하는 과정을 거치면 된다. 이 결과를 수식으로 구해주면 된다.
(C번) 점수를 최대로 https://www.acmicpc.net/problem/29767
$S$를 $A$의 누적합이라 하자. 그럼 더블카운팅적으로 생각했을 때 $S_i$중 가장 큰 $K$개를 더하는 것이 답이 된다.
(D번) 팰린드롬 이름 https://www.acmicpc.net/problem/29768
문제를 잘못 읽어서 풀게 된 그런 문제인데, 원래 문제 풀이의 증명이 상당히 재밌다. 길이 $n$의 문자열의 부분문자열 중 distinct한 팰린드롬의 개수는 최대 $n$개임은 들어본 적이 있을 것이다(구성은 그냥 같은 문자를 $n$개 쓰면 된다). 증명은 잘 모르고 있었는데, 선배들한테 들은 것은 다음과 같다.
수학적 귀납법을 쓸건데, $P_n$을 길이가 $n$일 때 최대라 하자. 그럼 여기서 문자를 하나 추가했을 때 생기는 팰린드롬의 개수가 최대 1개임을 보이면 된다. 마지막 문자가 추가된 상황에서, 가장 긴 팰린드롬 suffix를 하나 잡아보자. 그럼 이제 마지막 문자를 포함하는 팰린드롬은 모두 이 suffix 안에서 등장할 것이다. 만약 가장 긴 suffix보다 더 짧은 suffix에서 팰린드롬이 등장한다면, 이는 가장 긴 suffix의 prefix에도 등장함을 이 suffix가 팰린드롬임을 통해서 보일 수 있다. 즉, 2개 이상 등장할 수 없다.
그래서 그냥 a를 쭉 붙이면 된다.
(E번) 가짜 금화 찾기 https://www.acmicpc.net/problem/32259
제한이 $2^n$꼴이라 사고가 이분탐색 쪽으로 빠지기 쉬운데, 구간을 3개로 쪼개도 어떤 구간에 답이 있는지 알 수 있음을 알 수 있다. 그래서 삼분탐색을 할 수 있다.
(F번) 분필 도둑 https://www.acmicpc.net/problem/25428
선택된 모든 분필 등 중 최솟값만 가져갈 수 있다. 이를 잘 생각해보면, 모든 $A_i$에 대해, $A_i$보다 큰 정점만 살렸을 때 생기는 connected component들에 대해서 각 크기에 $A_i$를 곱해준 것 중 최댓값이 답이 될 것이다. 이는 간선이 연결 된 정점 중 $A_i$가 작은 값을 기준으로 간선을 정렬해주고 유니온 파인드를 사용해서 해결해 줄 수 있다.
(G번) 나비와 전봇대 (Easy) https://www.acmicpc.net/problem/30409
선분이 교차할 수 없고, 길이의 합이 최대라는 것은, 현재 연결 가능한 것들 중 가장 가까운 것에 연결해주는 것이 이득이라는 뜻이다.
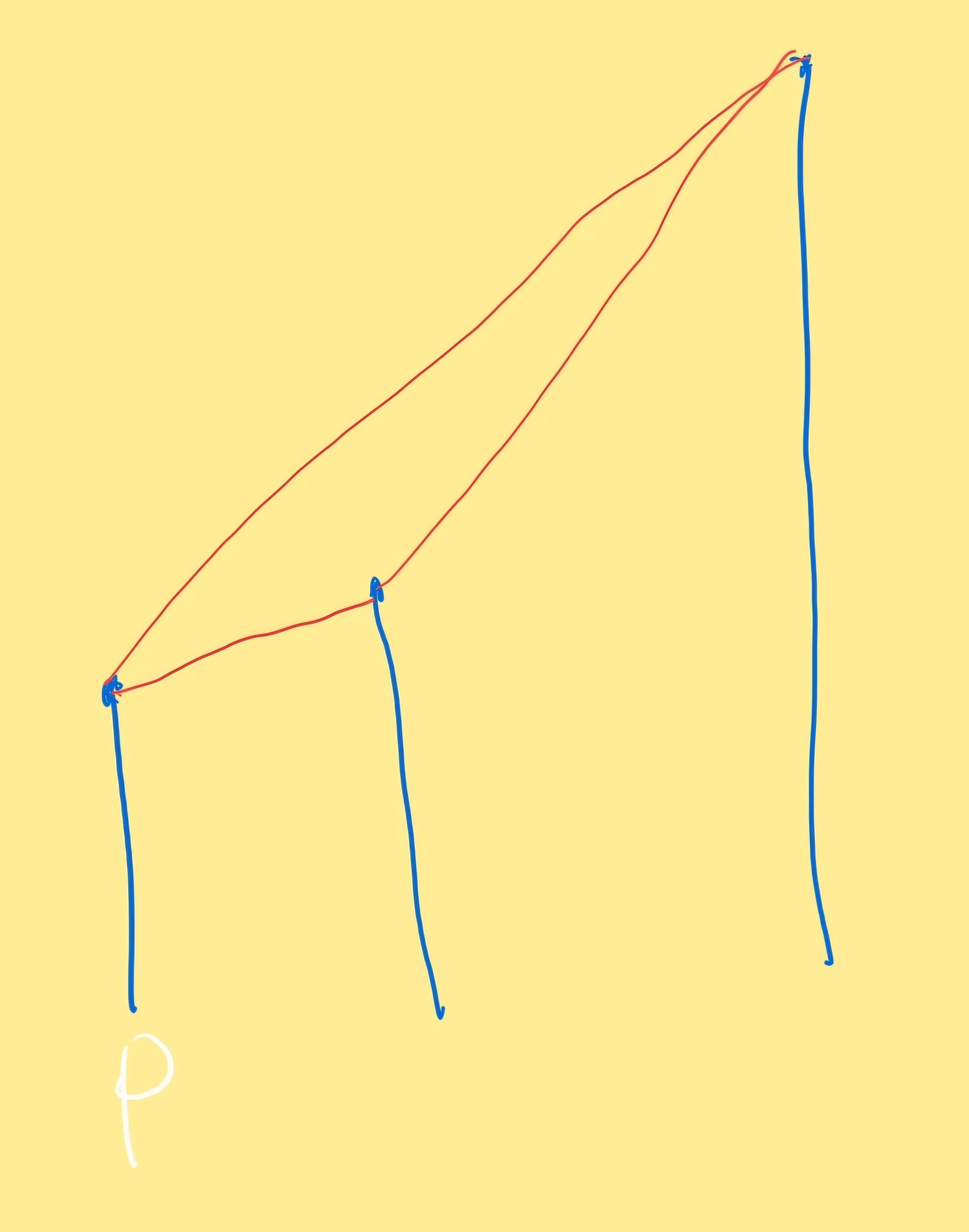
이는 삼각형의 빗변보다 나머지 두 변 길이의 합이 더 크다는 것을 생각해보면 된다.
또 비용이 최소라는 것은, 다음 그림과 같은 경우에서,
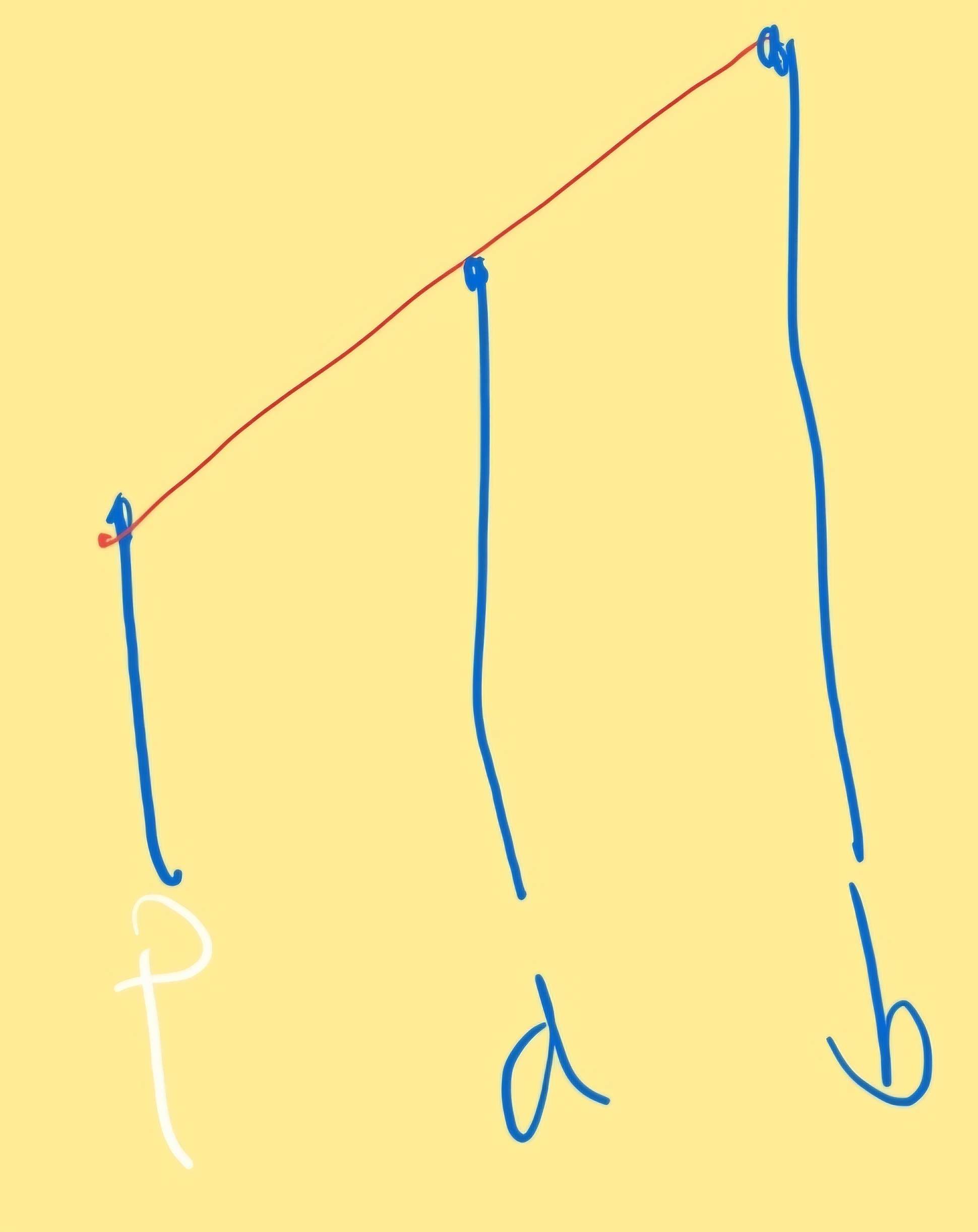
$p \rightarrow b$를 연결해주고 $a \rightarrow b$를 연결해줘야 함을 의미한다. 비용은 제곱이고, $x^2 + y^2 \leq (x + y)^2$임을 생각해보면 된다.
이는 각 전봇대마다 오른쪽으로 가는 비용과 왼쪽으로 가는 비용을 dp로 구해주면 된다.
왼쪽으로 가는 비용을 구해주는 방법만 설명해보자면, $c(i, j)$를 $i$와 $j$를 연결할 때 생기는 비용이라 하자. 그리고 $p$를 $j < i$이고 $H_j \geq H_i$인 $j$중 최댓값이라 하자. 그럼 $dp_i = dp_p + c(i, p)$가 되고, 이러한 $p$는 이분탐색이나 세그나 스택 등을 사용해서 구해줄 수 있다.
(H번) 문자열 구성하기 https://www.acmicpc.net/problem/32526
우선 나는 이 문제의 증명을 모른다는 것을 말하고 풀이를 서술하겠다.
적당한 나이브를 짜고 돌려보면 $n$이 소수일 때 $k \in \{ 0, n - 1 \}$일 때만 가능함을 추측해 볼 수 있다.
또, 어떤 $a \leq \frac{n}{2}, a | n$ 에 대해, $a - 1, a$또한 답이 가능함을 알 수 있다. 이는 $a^nb$나 $a^n b a^n$같은 문자열을 여러개 붙이면 된다.
(I번) 3개의 배열과 트리 https://www.acmicpc.net/problem/33014
사고의 흐름을 적어보자면,
랜덤한 배열 두개가 주어진다는 조건은 우선 무시하고, 첫번째와 두번째 배열만 항상 주어진다고 생각해보자. 우선 각 배열안의 값들은 순서가 섞이지 않는다. 이는 인덱스라는 정보를 인코딩과 디코딩 때 사용할 수 있음을 의미한다. 트리는 $v$와 $v$의 부모 $p_v$의 튜플로도 표현할 수 있다. 이때 우리는 인덱스도 사용할 수 있으니, 그냥 $p_v$의 값만 배열의 $v$번째 인덱스에 저장해주면 된다. 그러나 가치의 합이 너무 커지는 문제가 생긴다. 우리는 배열을 두개 사용할 수 있기에, 두 정수로 이루어진 튜플 $(i, j), i \leq j$을 정수로 가는 함수 $f : (i, j) \rightarrow \mathbb{N^+}$를 구성해주면 된다. 이때 $i$와 $j$의 합이 작은 것부터 튜플을 구성해주면, 적당히 제한에 들어가는 합이 나온다. 정확한 수식은 모르겠으나, 이를 계산한 것을 돌려보니 제한 내에 들어온다는 것을 알 수 있었다. 첫번째 배열의 첫번째 인덱스엔 $0$을, 두번째 배열의 첫번째 인덱스엔 $1$을 기록해주자. 그럼 어떤 배열이 몇번째 배열인지 알 수 있을 것이고, 우린 트리를 디코딩 할 수 있다.
세번째 배열은 배열의 값을 모두 XOR한 결과에 $N$을 곱한 것이 답이 되는데, 잘 생각해보면 세번째 배열의 가치를 0으로 만들기란 굉장히 쉽다. $N - 1$개의 값만 저장하고 나머지 하나의 인덱스엔 $N - 1$개의 값들을 모두 xor한 값을 저장하면 되기 때문이다. 마침 우리는 첫번째 배열과 두번째 배열에서 $N - 1$개의 값들만 사용하기에, 이를 잘 활용해보는 방향을 생각해 볼 수 있다. 우선 원 문제는 어떤 배열이 몇번째 배열인지 알 수 없도록 주어진다는 것을 생각해보면, 첫번째 배열의 마지막 인덱스엔 0을, 두번째 배열의 마지막 인덱스엔 1를 추가해주자. 그럼 첫번째 배열과 두번째 배열이 주어졌을 땐 쉽게 해결할 수 있다. 세번째 배열이 주어졌을 때를 위해서, 각 배열을 차례대로 $A[], B[], C[]$라 할 때, $C[i] = A[i] \oplus B[i] (1 \leq i < N)$로 두면, 간단히 복원이 가능해다 (xor연산의 역원은 자기 자신임을 생각해보면). 이제 $C[N]$이 문젠데, $\oplus_{i=1}^{N-1} C[i]$ 가 $0$ 또는 $1$이면 어떤 배열이 어떤 배열인지 알 수 없어지기 때문이다. 이는 그냥 $0$ 또는 $1$이면 애초에 값이 엄청 작기 때문에 그냥 $3$같은걸 기록해주면 된다.
(J번) 서로 다른 최대 구간과 쿼리 https://www.acmicpc.net/problem/29770
$MR[i]$을 구간 $[i, MR[i]]$에 서로 다른 수만 있도록 하는 최댓값이라 하자. 이는 투포인터로 모든 $i$에 대해 구해줄 수 있다. 그럼 이제 쿼리 $l, r$은 $\max_{i \geq l} \{ \max(MR[i], r) - i + 1 \}$이 된다. $MR[i] > r, MR[i] \leq r$로 구분해주면 식이 간단해지고, 이는 2차원 쿼리가 되니까 오프라인 쿼리 + 스위핑을 하면서 세그로 처리해줄 수 있다.
(K번) 음악회 https://www.acmicpc.net/problem/29769
평균은 당연히 최댓값이 될 것이고, 그중 학생이 가장 많아야 하며, 학생의 수가 같다면 연주하는 학생의 번호 중 가장 작은 번호가 작을수록 좋다. 이는 연속된 구간을 관리하는 std::set이나 금광세그를 사용해 관리해줄 수 있다. 금광세그가 구현은 훨씬 편한 것 같다.
(L번) gcd 놀이 https://www.acmicpc.net/problem/33512
$K = 0$이면 gcd colvolution(https://codeforces.com/blog/entry/112346)을 사용해 계산해줄 수 있다. gcd convolution은 그 무시무시한 이름과 다르게 그렇게 어려운 내용은 아니다. 정수는 소인수분해를 고려한다면 무한 차원 벡터 같은 존재이고 poset이기에 sos dp와 같은 방법을 사용해줄 수 있다(sos dp는 n차원 누적합임을 생각해보자). OR convolution과 AND convolution을 sos dp로 하는 방법에 대한 글도 읽어보면 이해에 도움이 될 수 있다(https://codeforces.com/blog/entry/115438).
$K \geq 3$이라면 가능한 수의 최댓값이 $X$일 때 답은 $X - 1$이 될 것이다. 그냥 $X, X, 1$을 추가해주면 된다.
$K = 1, 2$가 문젠데, 우선 $K = 1$을 해결해보자.
수를 한개만 추가할 수 있기에, 최댓값을 늘리거나, 최솟값을 줄이거나, 아니면 둘다 최적에 가깝게 바꾸거나를 할 수 있을 것이다. 만약 gcd의 최댓값을 늘리고 싶다면, 이미 수열 $A$에 있는 값을 추가하는게 이득이다. 만약 수열 $A$에 존재하지 않는 값 $c$를 추가한다면 이때 추가되는 gcd의 값들은 전부 이미 $A$에 있는 수들의 약수들만 가능하기 때문이다. 그럼 $A$의 최댓값을 추가하면 되고, gcd의 최솟값을 줄이고 싶다면 $1$을 추가하면 된다. 이제 최댓값과 최솟값을 둘다 적당하게 바꾸는 경우에 대해 생각해볼 수 있는데, 사실 이러한 경우는 고려하지 않아도 된다. 케이스를 나눠보자.
1. $A$에 있는 수를 추가하는 경우
이때 gcd의 최솟값은 변하지 않을 것이고 (이미 $A$에 존재하는 수를 추가하였으니), 최댓값만 변할텐데, 그럼 그냥 $A$의 가장 큰 원소를 추가하면 된다.
2. $A$에 없는 수를 추가하는 경우
$c$를 추가한다 하면, 추가적으로 생기는 gcd 값들은 전부 $c$가 아닌 $c$의 약수가 될 것이다. 이중 최대를 $M$, 최소를 $m$이라 한다면, $M$의 배수는 $A$에 존재할 것이고, 그 값은 $M$의 두배 보다 크거나, 값이 $M$과 같다면 $c \geq 2M$일 것이다. 이때 gcd 최솟값이 줄어드는 양보다 그냥 $M$의 배수를 $A$에 추가했을 때 늘어나는 gcd 최댓값의 양이 더 크기 때문에 이는 손해다.
이제 $K = 2$인 경우를 보자. $A$의 최댓값을 $L$이라 하면 답의 상한은 우선 $L$로 잡을 수 있다. $L + 1, L + 1$을 추가해주면 된다. 잘 생각해보면 위와 같이 같은 수 두개를 추가해주는 것이 최적이다. 그러나 이번에는 최댓값과 최솟값 둘다 변하는 경우를 생각해줘야 하는데, $A$에 존재하지 않는 수를 추가해줄 수 있기 때문이다. 가능한 수의 최댓값 $X = 10^5$에 대해, $(X, X), (X - 1, X - 1), (X - 1, X - 2)$만 추가해주는 경우를 다 계산해보면 된다. 왜냐면 적어도 저 세 수 중 하나랑은 gcd가 1이 될 것이기 때문이다. 또는 $X$보다 작거나 같은 수들 중 가장 큰 소수까지 계산해보는 것도 비슷한 논리로 가능하다.
(M번) XOR 놀이 (https://www.acmicpc.net/problem/25431)
비트연산의 (최대/최소)를 물어보는 문제는 보통 가장 큰 비트부터 (on/off)시킬 수 있는지 확인해보는 그리디를 적용하면 된다. $2^k > \sum_{i=0}^{i < k} 2^i$ 라서. 이 문제에선 그걸 구간에 대해서 해줘야 하는데, 이는 세그의 각 노드에 std::set 같은 bbst를 넣거나 그냥 제곱근분할 같은걸 해주면 된다.
(N번) XOR 머신 (https://www.acmicpc.net/problem/33276)
재밌는 문제다. 여담으로 부분수열 XOR 합의 최댓값은 XOR basis라는 걸 통해 구해줄 수 있다고 하는데, 난 잘 모른다. 아마 인터랙터를 그걸로 짜지 않았나 싶다.
서로 다른 연산을 많이 사용하는 두개의 풀이를 사용해 문제를 해결해야한다.
$(A[1] \oplus A[2]), (A[1] \oplus A[3]), \dots, (A[1] \oplus A[N - 1]), (A[1] \oplus A[N])$ 와 같은 수열에서 부분수열 XOR 합의 최댓값을 구해주면 $A$에서 짝수 개수의 부분수열만 고려했을 때의 답과 같은 결과가 나온다. XOR의 역원은 자기 자신임을 생각해보면 $A[1]$을 포함하는 경우 다른 원소들을 홀수개 사용하는 모든 경우를 고려하고, $A[1]$을 포함하지 않는 경우 다른 원소들을 짝수개 사용하는 모든 경우를 다 고려하기 때문이다. 이는 첫번째 연산을 많이 사용한다.
다른 방법으론, $A$의 모든 원소들의 $k$번째 비트를 켜주고 (이때 $2^k$는 $A$의 최댓값보다 커야한다) $2^k + 2^{k + 1}$을 추가해준 다음 이들로 부분수열 XOR합의 최댓값을 구해주면 된다. 마지막 원소가 엄청 크기 때문에 이는 반드시 포함될 것이고, 그럼 나머지 원소들에서 $k$번째 비트가 꺼져있는 것이 이득이기에 짝수 크기의 부분수열만 고려해줄 것이기 때문이다. 이는 두번째 연산을 많이 사용한다.
(O번) 색깔 사각형과 쿼리 (https://www.acmicpc.net/problem/32766)