0. 서론
2학년 때 학교 프로젝트로 TSP에 대해 다룬 적이 있는데, 이와 관련하여 MDMTSP(814-3)에 대한 해결책을 요즘 찾고 있어 정리해볼까 한다. TSP(외판원 순회 문제)는 대표적인 NP-complete(결정 문제의 경우) 문제 중 하나이다. ps에선 흔히 bit dp라 불리는 테크닉을 처음 접할 때 많이 소개되곤 한다. $\mathcal{O}(N \cdot 2^N)$ 정도의 해결책은 널리 알려져 있지만 P = NP가 아닌 이상 다항 시간 해결책을 기대하긴 어렵다. 근사해를 구하기 위한 시도를 해볼 수도 있지만, 다항 시간 근사해 조차 구하기 힘들다. 그러나 TSP로 환원 되는 다양한 문제들이 존재하고 현실 세계에서 이에 대한 해결책이 필요한 경우가 있다. 이 글에서는 TSP를 해결하는 다양한 시도들에 대해 소개한다.
1. 소개
TSP는 간선의 가중치가 주어진 완전 그래프 $G = (V, E), w : E \rightarrow \mathbb{R}$가 주어질 때 사용한 간선 가중치의 합이 최소인 해밀턴 사이클을 찾는 문제이다. 가중치가 $L$ 이하인 해밀턴 사이클이 존재하는가? 에 대한 결정 문제는 NP-complete임이 알려져 있다. 이는 해밀턴 사이클에서 오는 환원이 존재하기 때문이다.
TSP를 해결하기 위한 시도들은 보통 특수한 경우에서 해결하거나 메타휴리스틱을 사용한다. 이에 대해 몇가지 알아보자.
2. TSP with monge cost
어떤 행렬 $C \in \mathbb{R}^{n \times m}$이 monge matrix(또는 monge array)라 함은 $1 \leq a < b \leq n$, $1 \leq c < d \leq m$ 에 대하여 $C(a, c) + C(b, d) \leq C(a, d) + C(b, c)$임을 의미한다. ps를 어느정도 접해본 사람이라면 이에 익숙할 것이다. 다수의 dp 최적화 알고리즘이 cost가 monge임에 기반을 두고 시작한다.
만약 TSP 간선의 가중치에 대한 행렬 $C \in \mathbb{R}^{n \times n}$이 monge matrix 이라면, 이 문제를 해결하는 다항 시간 알고리즘이 존재한다. 놀랍게도 $\mathcal{O}(N \log N)$ 시간에 해결할 수 있다!
추가) 만약 symmetric ($C(a, b) = C(b, a)$) 조건이 추가로 주어진다면 $\mathcal{O}(N)$에 해결하는 그리디 알고리즘이 존재한다. https://chaoxu.prof/posts/2014-12-13-tsp-supnick-matrix.html 참고
Theorem. 어떤 경로 $P$가 $\{ 1, i_1 < i_2 < i_3, \dots, < N > j_1 > j_2 > j _3, \dots \}$을 만족하면 이를 pyramidal 하다고 한다. pyramidal 한 optimal tour가 항상 존재한다.
proof.
어떤 optimal tour $P$를 가져오자. 일반성을 잃지 않고 $P$가 항상 $1$로 시작한다 하자. $P$를 두가지 부분으로 분리해보자.
(1) $1$에서 $N$으로 가는 경로
(2) $N$에서 $1$로 가는 경로
(1)을 오름차순 정렬하고 (2)를 내림차순 정렬한 것이 항상 더 좋거나 같음을 보이면 된다.
(1) 을 오름차순 정렬한 것이 항상 더 좋거나 같음을 보이자.
(1)이 크기 4인 경우
$\{ 1, i_2, i_1, N \}$일 때 $i_1 < i_2$라 하자. $C(1, i_1) + C(i_1, i_2) + C(i_2, N) \leq C(1, i_2) + C(i_2, i_1) + C(i_1, N)$은 참이다. 이는 monge matrix 정의에 의해 보일 수 있다.
$C(1, i_1) + C(i_1, i_2) \leq C(1, i_2) + C(i_2, i_1)$, $C(i_1, i_2) + C(i_2, N) \leq C(i_2, i_1) + C(i_1, N)$, $C(1, i_1) + C(i_2, N) \leq C(1, i_2) + C(i_1, N)$
비슷하게, 임의 크기의 경로를 정렬하면 항상 더 좋거나 같음을 보일 수 있다.
(2) 를 내림차순 정렬하는 것 또한 비슷하게 보일 수 있다.
그럼 다음과 같은 DP를 생각해볼 수 있다. $D(i, j)$를 $1, 2, \dots, \max(i, j)$까지의 도시만 고려했을 때, $i$부터 $1$까지 내림차순으로 방문하고, $1$부터 $j$까지 오름차순으로 방문할 때 최소 가중치라 정의하자. TSP의 정답은 $\min_i \{ D(i, N) + C(N, i), D(N, i) + C(i, N) \}$이 될 것이다.
다음과 같은 관찰을 통해 상태 개수를 줄일 수 있다.
lemma. $|i - j| = 1$인 $D(i, j)$들만 고려해도 된다.
proof.
$i < j$라 하자. 이때 $i \neq j - 1$ 이라면 $1$에서 $j$로 가는 경로에 $j - 1$이 있을 것이고, 이는 $j$ 바로 전에 있다(이 경로가 오름차순 정렬 되어있음을 생각하자). 그렇다면 이 상태는 $D(j, j - 1)$로 표현 가능하다.
$i > j$ 일 때도 같은 논리를 사용하여 $j \neq i - 1$일 경우 $D(i - 1, i)$로 이 상태를 표현해줄 수 있다.
상태 개수가 $O(N)$개로 변하였고, TSP의 정답은 $\min \{ D(n - 1, n) + C(n, n - 1), D(n, n - 1) + C(n - 1, n) \}$이 된다.
$D(i, i + 1)$을 다음과 같이 분해해보자. $j$에서 $i + 1$로 가는 경로, $i$에서 $j + 1$로 가는 경로, $D(j + 1, j)$. 이때 $i$에서 $j + 1$로 가는 경로는 연속적임을 관찰하면 좋다. 즉 이 경로는 $\{ i, i - 1, i - 2, \dots, j + 2, j +1 \}$ 이다.
다음과 같은 점화식이 성립한다.
$D(i, i + 1) = \min_{j < i} D(j + 1, j) + C(j, i + 1) + \sum_{k = j + 1}^{i - 1} C(k + 1, k)$
$D(i + 1, i) = \min_{j < i} D(j, j + 1) + C(i + 1, j) + \sum_{k = j + 1}^{i - 1} C(k, k + 1)$
$F(i) = D(i, i + 1)$, $G(i) = D(i + 1, i)$라 하자.
$A(i, j) = C(i, j + 1) + \sum_{k = i+ 1}^{j - 1} C(k + 1, k) (i < j)$이고
$B(i, j) = C(j + 1, i) + \sum_{k = i + 1}^{j - 1} C(k, k + 1) (i < j)$라 하면
$F(i) = \min_{j < i} G(j) + A(j, i)$이고
$G(i) = \min_{j < i} F(j) + B(j, i)$이다.
이때 $A$와 $B$가 각각 monge matrix임은 쉽게 보일 수 있고, $F$와 $G$를 monotone queue optimization (https://gubshig.tistory.com/45 참고) 등을 통해 $\mathcal{O}(N \log N)$ 시간에 계산해줄 수 있다.
3. metric이 주어졌을 때의 다항 시간 근사 알고리즘
이에 관련하여 한국어로 된 좋은 자료가 존재한다 (https://gazelle-and-cs.tistory.com/18 https://gazelle-and-cs.tistory.com/24).
어떤 문제의 PTAS(Polynomial-Time Approximation Scheme)란 어떤 $\rho > 0$에 대해 최적해의 $\rho$배를 넘지 않는 해를 다항 시간에 구하는 알고리즘을 말한다.
일반적인 TSP의 PTAS는 아쉽게도 존재하지 않는다. 해밀턴 사이클에서 오는 간단한 환원이 존재하는데, 해밀턴 사이클을 찾고자 하는 그래프 $G = (V, E)$를 가지고 새로운 가중 완전 그래프 $G' = (V, E')$, $w : E' \rightarrow \mathbb{R}$를 만든다. 이때 $w$를 다음과 같이 정의한다.
$w((u,v)) = \left\{ \begin{array}{rl} 0, & \text{if } (u,v) \in E(G), \\ 1, & \text{if } (u,v) \notin E(G). \end{array} \right.$
이때 $G$에서 해밀턴 사이클이 존재한다면 $G'$에서 TSP의 최적해는 $0$일 것이다. 만약 TSP의 어떤 PTAS가 존재하여 $\rho$-approximation을 구할 수 있다면 그 알고리즘은 $G'$에서 가중치가 $0$인 해를 찾을 수 있을 것이다. 해밀턴 사이클은 NP-complete 문제이고, 즉 일반적인 TSP의 PTAS는 존재하지 않는다.
특수한 경우의 TSP에서는 PTAS가 존재하는데, 이에 대해서 알아보자.
metric space란 어떤 조건들을 만족하는 거리 함수 $d : M \times M \rightarrow \mathbb{R}^+$ 가 주어진 공간을 말한다.
- $d(x, x) = 0$
- $d(x, y) = d(y, x)$
- $d(x, z) \leq d(x, y) + d(y, z)$
이는 가장 보편적으로 생각되는 거리를 추상화했다고 생각해도 좋다. 유클리드 거리, 그래프에서의 최단거리 등등 많은 거리 함수들이 metric space의 조건을 만족한다. 이제부터 TSP에서의 거리가 metric을 만족한다는 가정 하에 다항 시간 근사를 구해보자.
조금 뜬금없을 수 있지만, MST(Minimum Spanning Tree)에 대해 생각해보자. MST의 가중치는 TSP의 최적해보다 항상 작거나 같다(그렇지 않다면 최적해의 사이클에서 간선 하나를 제거해 스패닝 트리를 만들면 되니).
이제 이 트리에서 임의의 dfs ordering을 매겨 이 순서대로 TSP의 사이클로 만들면 이 해의 가중치는 MST의 2배보다 작거나 같다.

편의상 노드의 번호와 dfs ordering이 같다고 하자. 이 트리에서 dfs ordering 순서대로 방문한다면,

이런 해가 만들어질 것이다. metric의 성질에 의해 트리에서의 tree edge가 아닌 것들의 길이의 합이 tree edge들의 길이의 합보다 작거나 같음을 보일 수 있기에 이 해가 MST의 2배 이하임을 보일 수 있다. $(4, 5)$를 생각해보면 이 간선의 길이는 $(1, 2), (2, 3), (3, 4), (1, 5)$의 길이의 합보다 작거나 같다.
$d(1, 3) \leq d(1, 2) + d(2, 3)$, $d(1, 4) \leq d(1, 3) + d(3, 4)$, $d(4, 5) \leq d(4, 1) + d(1, 5)$를 만족하기 때문이다.
결과적으로 이렇게 찾은 해는 TSP의 $2$-approximation이 된다(MST의 가중치는 TSP의 최적해보다 항상 작거나 같음에 의해).
완전 그래프의 MST는 $\mathcal{O}(V^2)$시간에 구할 수 있고, 만약 정점들 사이의 거리가 유클리드 거리라면 들로네 삼각분할 등을 사용하여 최적화 할 수도 있을 것이다.
위에서 설명한 알고리즘을 보완하기 위해 가중 일반 매칭을 이용해 $1.5$- approximation을 하는 방법도 존재한다(Christofides' Algorithm). $1.5 - 10^{-32}$(...) approximation (https://arxiv.org/pdf/2007.01409)이 내가 알고 있는 최선이다.
4. 휴리스틱
휴리스틱은 문제의 최적해를 유의미한 자원 소모량으로 얻어낼 수 없을 때, 근사해를 구하기 위해 사용된다. NP-hard 문제들은 다항 시간 해법이 존재하지 않기에, 휴리스틱을 사용한 해법들이 많이 사용된다.
TSP는 상태의 개수가 $\mathcal{O}(N!)$이므로 일반적인 완전탐색은 힘들다. TSP를 위해 만들어진 휴리스틱 2개와, TSP에 사용할 수 있는 범용적인 메타휴리스틱 2개를 소개한다.
4-1. $k$-opt 알고리즘
우선 임의의 경로를 하나 구하자. 그 경로에서 간선을 $k$개 교체하여 더 좋은 경로를 만들 수 있으면 교체를 하고 이를 반복한다. 일종의 hill climbing 이다. $k$가 증가할 때 가능한 간선 교체의 수가 지수적으로 늘어남으로 보통 $k = 2, 3$을 사용하고 $4$를 사용하는 경우도 있다.
4-2. Lin Kernighan Heuristic
LKH(Lin Kernighan Heuristic)은 $k$-opt에서 $k$를 adaptive하게 선택하는 알고리즘이다. 단 거리함수가 symmetric하다는 전제가 필요하다. 기본적인 토대는 hill climbing과 유사한 그리디 알고리즘이지만, 다른 메타휴리스틱과 결합하여 사용할 수 있다는 특징이 있다. 간단한 알고리즘을 https://arxiv.org/pdf/1003.5330 에서 찾아볼 수 있다.
4-3. Simulated Annealing (담금질 기법)
담금질 기법은 ps에서 가장 많이 보이는 메타휴리스틱이다. ps에서 사용되는 SA(Simulated Annealing)에 대한 설명은 많은 자료가 존재한다 (https://ryute.tistory.com/35). 간단히 설명하겠다.
다음과 같은 식을 기반에 둔다.
$p = \exp(\frac{E_1 - E_2}{k \cdot t})$
이때 $p$는 인접 상태로 이동할 확률, $\exp$는 지수함수, $E_1$은 현재 상태의 가중치, $E_2$는 인접 상태의 가중치, $k$는 임의의 상수, $t$는 현재 지난 시간을 의미한다. 이 식을 해석해보자. 편의상 가중치의 최소가 최적해인 최소화 문제(Minimization problem)에 대해 생각해보자. $E_1 > E_2$인 경우에는 $p > 1$이고 이는 다음 상태의 가중치가 더 작을 경우 무조건 그 상태로 이동한다는 것을 의미한다. $E_1 < E_2$인 경우에도 다음 상태로 이동할 확률이 존재하는데, 이는 차이가 클수록, 시간이 지날수록 감소한다. 탐색 초반에는 적극적으로 다양한 상태를 시도해보고, 시간이 지날수록 소극적이게 된다는 것을 의미한다. 메타휴리스틱 알고리즘이 해결해야할 문제는 극솟값(Local minimum)에 빠지지 않는 것인데, SA는 이를 잘 탈출한다. 다음 상태가 더 좋지 않을 경우에도 그 상태로 이동할 확률이 존재하기 때문이다. SA를 적용시키기 위해서는 몇가지 고려사항들이 존재한다. 우선 인접 상태를 잘 정의해야 한다. 인접 상태와 현재 상태의 차이가 너무 크다면 랜덤하게 탐색하는 것과 다를 것이 없기 때문이다. 시간의 증감 $\Delta t$나 상수 $k$와 같은 하이퍼 파라미터를 튜닝하는 것도 중요하다.
보통 TSP에서는 인접 상태를 현재 경로에서 임의의 간선 $k$개를 변경한 상태로 둔다. 일종의 $k$-opt 알고리즘의 변형이라 볼 수 있다. 보통 $2$를 $k$로 가장 많이 사용한다. 보다 더 큰 $k$를 사용하면 인접 상태가 현재 상태에 비해 너무 많이 변하기에 올바른 해를 구하기 어려워하는 양상을 띈다. 필자는 $4$를 사용해보았지만 좋은 해를 구하기 어려웠었다.
4-4. DLAS(Diversifed Late Acceptance Search)
https://arxiv.org/pdf/1806.09328 2018년에 나온 최신 논문이다. LAHC (Late Acceptance Hill Climbing)을 보완한 알고리즘으로 다소 복잡한 acceptance strategy를 가진다. DLAS는 전 상태들의 가중치들을 저장하는 배열 $A[]$를 관리한다. 보통 크기 $5$를 사용한다.
SA과 유사하게 인접 상태를 구하자. 이 인접 상태의 가중치를 $F$, 현재 상태의 가중치를 $S$라 하자. 인접 상태를 받아들이는 acceptance strategy는 다음과 같다. 현재 상태와 가중치가 같거나($S = F$) 배열 $A[]$의 최댓값 보다 가중치가 작으면($F < \max A$) 이 상태를 받아들인다(accpet).
배열의 값을 갱신하는 방법은 다음과 같다. 현재 반복 횟수를 $l$이라 하자. $F > A[l \mod 5]$ 이거나 $F < S$이고 $F < A[l \mod 5]$이면 $A[l \mod 5] \leftarrow F$로 값을 갱신한다.
이 단순한 방법은 꽤 강력한 성능을 보인다. SA의 문제점인 처음에는 다양한 해를 탐색하지만 시간이 지날수록 local optimum을 잘 빠져나오지 못하는 부분을 어느정도 보완할 수 있다. DLAS가 보다 더 다양한 해를 탐색하기 때문이다.
DLAS와 SA의 비교
https://www.acmicpc.net/problem/20138
유클리드 TSP를 다루는 이 문제에서 DLAS와 TSP의 성능을 비교해보았다.
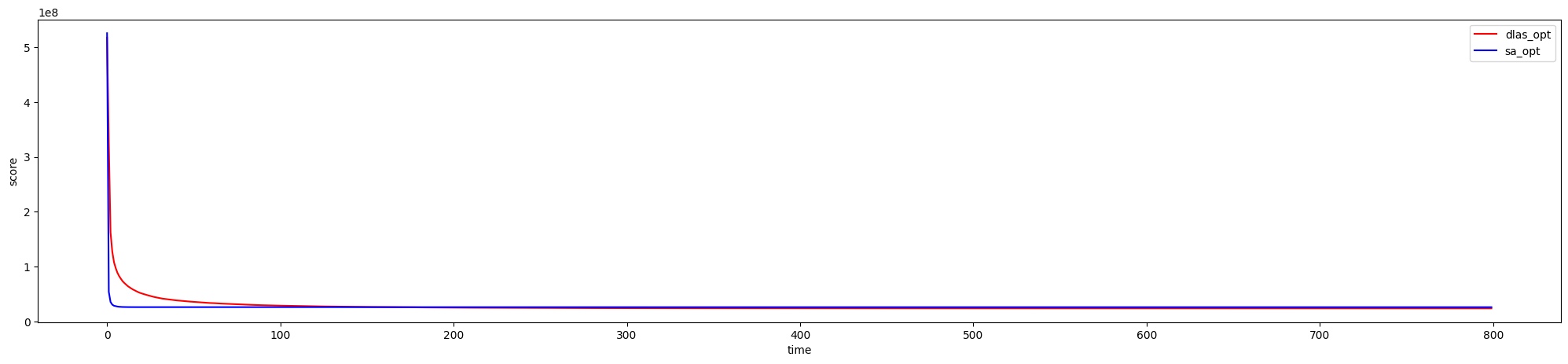
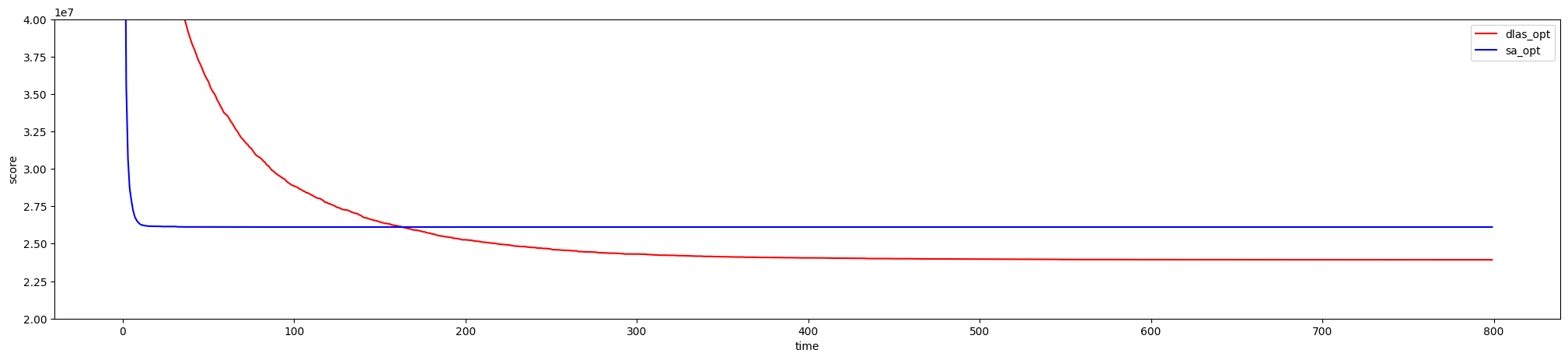
초반에는 SA가 우월한 성능을 보여주지만, 충분히 많은 시간이 지날 경우 DLAS가 보다 더 좋은 해를 찾음을 확인할 수 있었다.
참고한 자료
Perspectives of Monge properties in optimization (Rainer E. Burkard, Bettina Klinz, Riidiger Rudolf 1996)
'알고리즘' 카테고리의 다른 글
| 오프 향유회 후기 (0) | 2024.09.01 |
|---|---|
| MDMTSP(814-3) 정리 (1) | 2024.08.26 |
| 리차오 트리의 정상화 (2) | 2024.07.29 |
| 2024 정보올림피아드 고등부 2차 (22) | 2024.07.14 |
| abc339 - 블루를 가다 (1) | 2024.02.03 |